[Noise 入門 #04] Perlin Noise のアルゴリズムを図解で理解する

はじめに

Noise 入門 4回目。

今回は、Perlin Noise のアルゴリズムを図解で理解する。

前回の記事：

[Noise 入門 #03] ノイズを設計する5つのパラメータ（Frequency / Amplitude / Octave / Lacunarity / Gain）

ノイズの形と性質を完全に決める5つのパラメータ（frequency, amplitude, octave, lacunarity, gain）を詳細に解説。ノイズアート・地形生成・雲・炎・Fog・Shader 実装など、全ての procedural 表現の基礎 …

https://humanxai.info/posts/noise-intro-03-noise-parameters/

1. Perlin Noise は何が特別なのか？

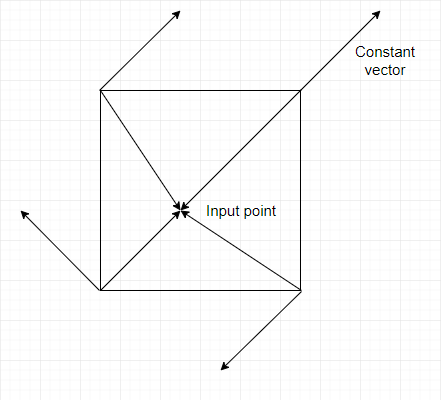
Perlin Noise が広く使われる理由は、 「ランダムなのに、破綻しない滑らかさ」 にある。

ゲーム・映画・VFX・CG の自然表現では、 不連続な乱数（Random） では絶対に太刀打ちできない。

Perlin Noise はこの“自然な連続性”を作るために、 内部で 4 つの処理を連鎖させている。

Perlin Noise を構成する4つの技術

1. 格子（Grid） 空間をタイル状に区切って、どのセルにいるかを判定する。

2. 勾配ベクトル（Gradient） 乱数ではなく “乱数方向ベクトル” を格子点に置く。

3. 内積（Dot）で影響度を計算 座標から格子点へのベクトルと勾配の内積が「影響度」になる。

4. 補間（fade）で滑らかに混ぜる Quintic 補間（5次式）で“破綻のない連続性”を作る。

この仕組みが自然を作る理由

Perlin Noise は、 隣接する値同士が必ず滑らかに変化するという性質を持つ。

だから：

• 2D化 → 地形・雲・水面
• 3D化 → ボリューム雲・煙・霧・洞窟
• 時間軸追加 → 動く雲・波・火炎

すべてが自然に見える。

乱数を“自然の形に変換する数学” それが Perlin Noise の本質。

2. まず全体フロー（図で理解）

Perlin Noise の内部処理は、 ひとつの座標 (x, y) がどのように “滑らかな値” に変換されるのか を追うだけで全体が理解できる。

以下の流れをつかめば、Perlin Noise の本質はほぼ掴んだと言っていい。

Perlin Noise の5ステップ（図解）

1) 座標 (x, y) がどのセルに入っている？
     → 左上 / 右上 / 左下 / 右下 の 4 点を取得

2) 各格子点に「ランダム勾配ベクトル」を配置する
     （乱数“値”ではなく、乱数“方向”ベクトル）

3) 座標 (x, y) から各格子点への方向ベクトルを求める

4) この2つのベクトルの「内積」で“影響度”を算出
     → 勾配ベクトルと方向の一致度（= 影響の強さ）

5) x方向 → y方向の順に fade() 補間でスムーズに混ぜる
     → Quintic（5次式）で連続性を保証

これで何が得られるのか？

滑らかに連続した値。 これが Perlin Noise の唯一にして最大の特徴。

乱数は “点ごとにバラバラ”。 Perlin Noise は “点の間が自然につながる”。

だから：

• 地形
• 雲
• 水面
• 霧・炎
• 魔法陣の揺らぎ
• Procedural Texture

すべての基礎として使われている。

3. ステップ①：グリッド（格子）

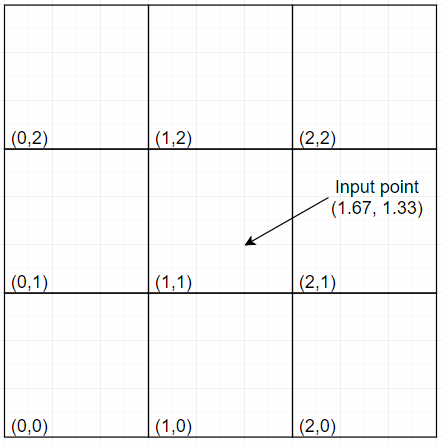
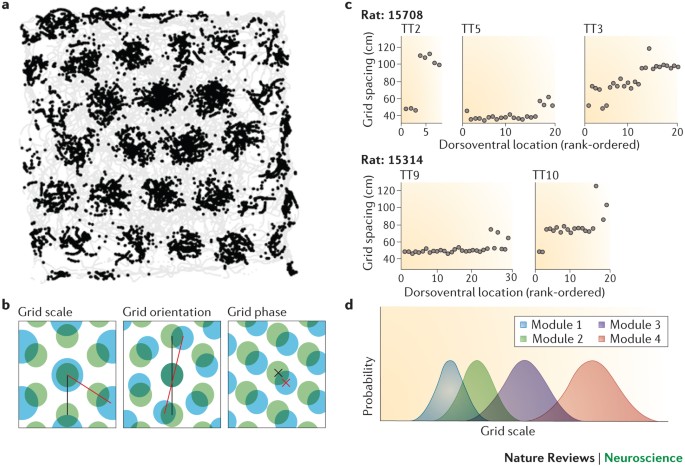
Perlin Noise はまず、 “空間をタイル状に区切る” ところから始まる。

どの座標 (x, y) も、 必ずこの格子の どれか 1 マスの中に存在している。

そのため、まずは (x, y) が含まれるセルの 「左下／右下／左上／右上」の4つの格子点を特定する。

グリッド構造（概念図）

(ix, iy)     (ix+1, iy)
   ●-----------●
   |           |
   |   (x,y)   |
   ●-----------●
(ix, iy+1)   (ix+1, iy+1)

ここで出てくる (ix, iy) は「整数化したインデックス」。

ix = floor(x)
iy = floor(y)

この 4 点が「ノイズ値を決める4つの親点」 になる。

なぜ格子が必要なのか？

理由はシンプルで：

グリッドがあることで、 ノイズの“滑らかさの境界”をコントロールできるから。

もし格子がなければ、 ランダムが無秩序に散らばるだけで、 自然界のような“連続性”は作れない。

Perlin Noise の全アルゴリズムは この「格子点からの影響」をどう混ぜるか、に尽きる。

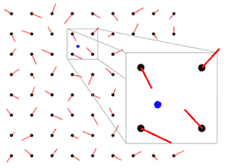
4. ステップ②：勾配ベクトル（Gradient Vector）

Perlin Noise の最重要ポイントのひとつが、 格子点に「乱数値」ではなく「乱数ベクトル」を置く という発想。

これは“値ノイズ（Value Noise）”との決定的な違い。

各格子点にランダム方向のベクトルを置く

格子点ごとに、長さ1前後のランダムベクトルを割り当てる：

( 1.0,  0.0)
( 0.7,  0.7)
(-0.6,  0.8)
(-1.0,  0.3)
...

向きはランダムだが、 大きさ（norm）は一定に“正規化（normalize）”しておく → これによりノイズのばらつきが整い、滑らかな特性が出る。

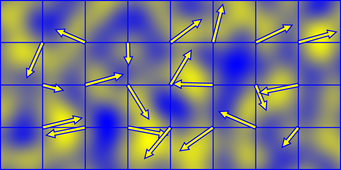
なぜ“乱数ベクトル”なのか？（ここが本質）

“ランダムな数”を置くだけなら Value Noise と同じ。 しかし Value Noise は 境界で不自然な段差が出る。

Perlin はこれを避けるために：

• 格子点には“方向”を持つベクトルを置き
• その方向が座標にどれだけ寄与するか（内積）を使った

このアプローチにより、 隣接セルをまたいでも連続性が保たれる。

まとめ：Perlin の「滑らかさ」は勾配ベクトルが作っている

• 各格子点に置かれた勾配方向
• 座標との方向差の内積
• その後の smoothstep/quintic 補間

この3段構えで、 “不自然な境界のないノイズ”が完成する。

5. ステップ③：内積（Dot Product）で影響度を計算

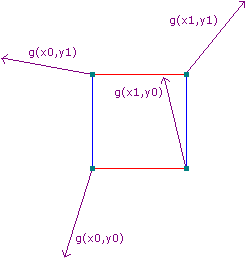
Perlin Noise の「滑らかな変化」を作り出すのは、 “勾配ベクトル × 位置ベクトル” の内積。

これが “その格子点が (x, y) にどれだけ寄与するか” を定量的に決めるコア処理になる。

① 座標 (x, y) から格子点への方向ベクトルを求める

座標と格子点の距離を取り、方向ベクトルを作る：

dx = x - ix
dy = y - iy

※ (ix, iy) は格子点の整数インデックス。

② 勾配ベクトルとの内積を取る

格子点が持つ“ランダム方向ベクトル”を gradient とすると：

influence = dot(gradient, (dx, dy))

内積の性質：

• 向きが似ているほど値が大きくなる
• 向きが逆なら負になる
• 距離が小さければ影響も小さくなる

③ これが “格子点の影響度” に変換される

内積の結果は、 (x, y) がどの方向へ向いているかに応じて 連続的に変化する。

このおかげで：

• Value Noise のような“境界の段差”が出ない
• 勾配方向に沿って 自然な滑らかさ が生まれる
• fade() 補間との相性が抜群になる

Perlin Noise の“自然さ”は、この内積計算が作っている。

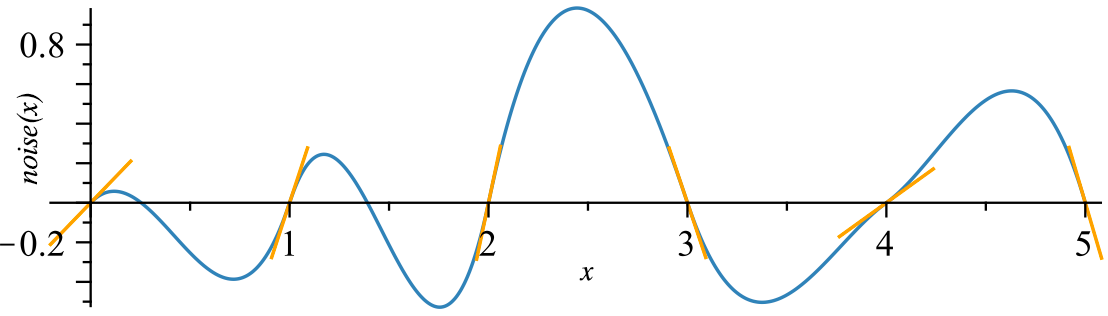
6. ステップ④：fade() 補間

Perlin Noise の“自然さ”の核は、 補間（interpolation）をどう行うか にある。

ただ線形補間（lerp）すると境界が硬く、 ノイズが「人工的な縞模様」になってしまう。

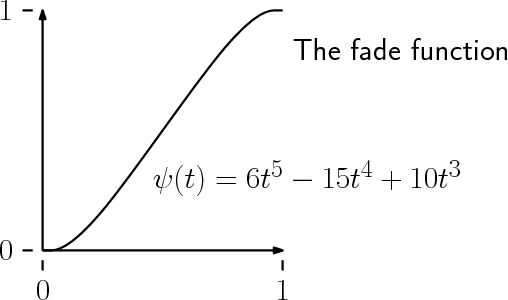
これを解決するために、Ken Perlin は “5次多項式（Quintic）補間” を導入した。

fade 関数（Quintic）

f(t) = 6t^5 - 15t^4 + 10t^3

この関数の特徴：

• 両端（0 と 1）の勾配が 0 に収束する
• つまり 滑らかに始まり、滑らかに終わる
• 境界の破綻（ノイズの継ぎ目）が完全に消える

この性質により、滑らかで自然なノイズ が成立する。

補間は “2段階” で行われる

① x方向での補間（水平補間）

まず、左右の影響度を fx で補間する：

nx0 = lerp(influence00, influence10, fx)
nx1 = lerp(influence01, influence11, fx)

fx = fade(x - ix) で滑らかさを確保。

② y方向での補間（垂直補間）

次に、上下方向を fy で補間する：

n = lerp(nx0, nx1, fy)

fy = fade(y - iy) も同様に quintic を使う。

最終結果：破綻のないスムーズなノイズ

• 4つの格子点からの“影響度”
• Quintic 補間の2段階合成
• 内積＋fade が織りなす方向性と滑らかさ

これが合わさって、 地形・雲・水・炎の基礎となる Perlin Noise が完成する。

Perlin Noise の本質は、 “ランダムを自然に見せる数学” にある。

7. 実装（疑似コード）

ここまでで Perlin Noise の数学は理解できた。 次は それをどうコードへ落とし込むか。

この疑似コードは：

• R3F（React-Three-Fiber）
• GLSL（ShaderMaterial）
• Unity（C#）
• Unreal（HLSL / Blueprint）
• Python / Rust / C++ など あらゆる環境で共通して使える“本質部分”。

Perlin Noise の最小実装（疑似コード）

function perlin(x, y) {
  // ① 格子点（整数座標）を求める
  const ix = Math.floor(x);
  const iy = Math.floor(y);

  // ② 小数部分（セル内の相対位置）
  const fx = fade(x - ix);
  const fy = fade(y - iy);

  // ③ 4つの格子点の勾配ベクトルを取得
  const g00 = gradient(ix,   iy  );
  const g10 = gradient(ix+1, iy  );
  const g01 = gradient(ix,   iy+1);
  const g11 = gradient(ix+1, iy+1);

  // ④ 内積（影響度）
  const d00 = dot(g00, x-ix,   y-iy);
  const d10 = dot(g10, x-ix-1, y-iy);
  const d01 = dot(g01, x-ix,   y-iy-1);
  const d11 = dot(g11, x-ix-1, y-iy-1);

  // ⑤ x方向の補間
  const nx0 = lerp(d00, d10, fx);
  const nx1 = lerp(d01, d11, fx);

  // ⑥ y方向で補間（最終値）
  return lerp(nx0, nx1, fy);
}

このコードが意味すること

ここに出てくる要素はすべて次につながる：

つまり：

Perlin Noise の理解 =
FBM / Domain Warping / Procedural World への入口に完全到達したということ。

8. #05 への橋渡し — ここから“地形”になる

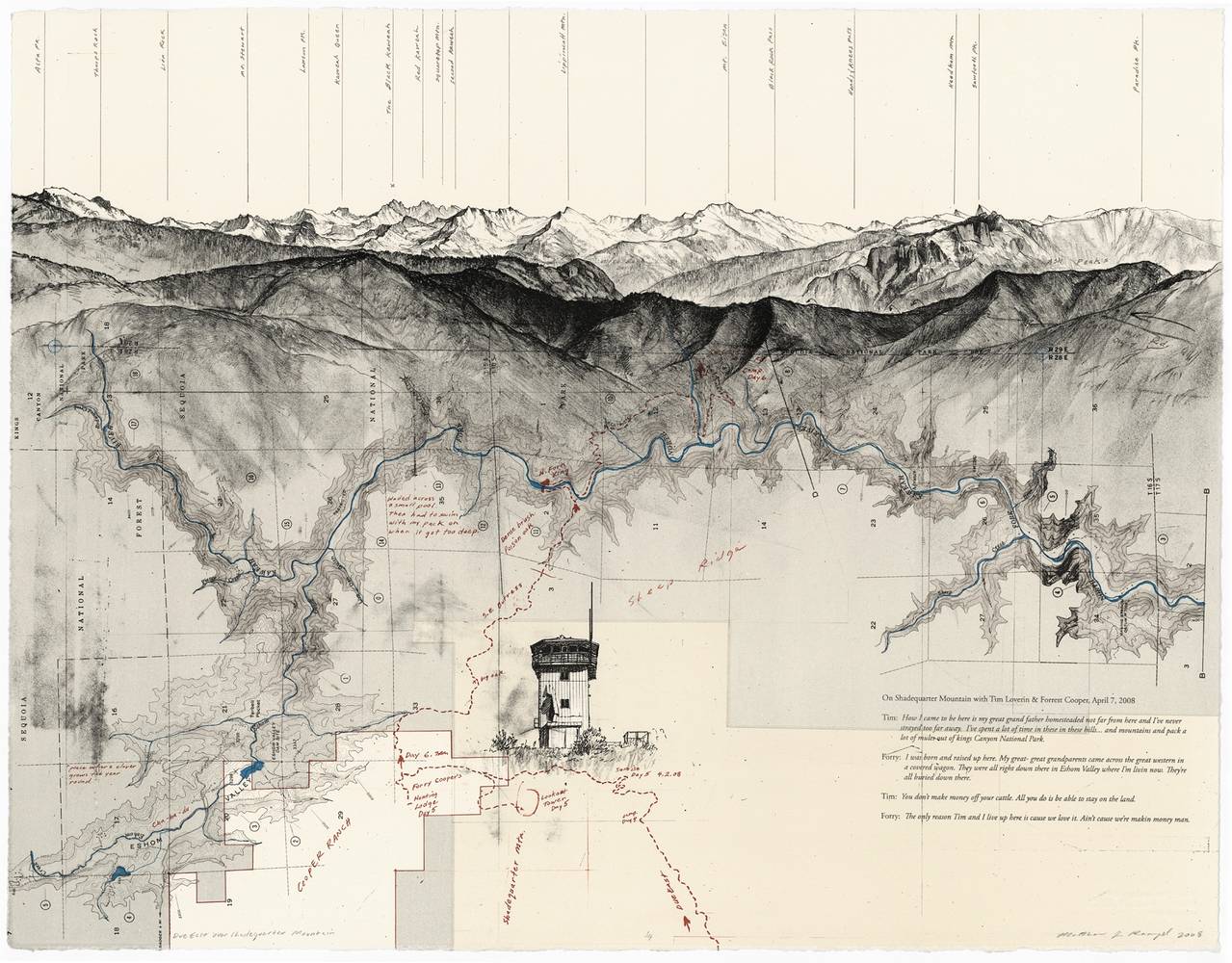
Perlin Noise を 1回だけ呼んでも、それはまだ 「自然っぽい模様」 に過ぎない。

地形・雲・水・炎の“生命感”は、 Perlin を“重ねる”ことで初めて生まれる。

FBM（Fractal Brownian Motion）とは？

以下を繰り返して合計するだけの、驚くほどシンプルなアルゴリズム：

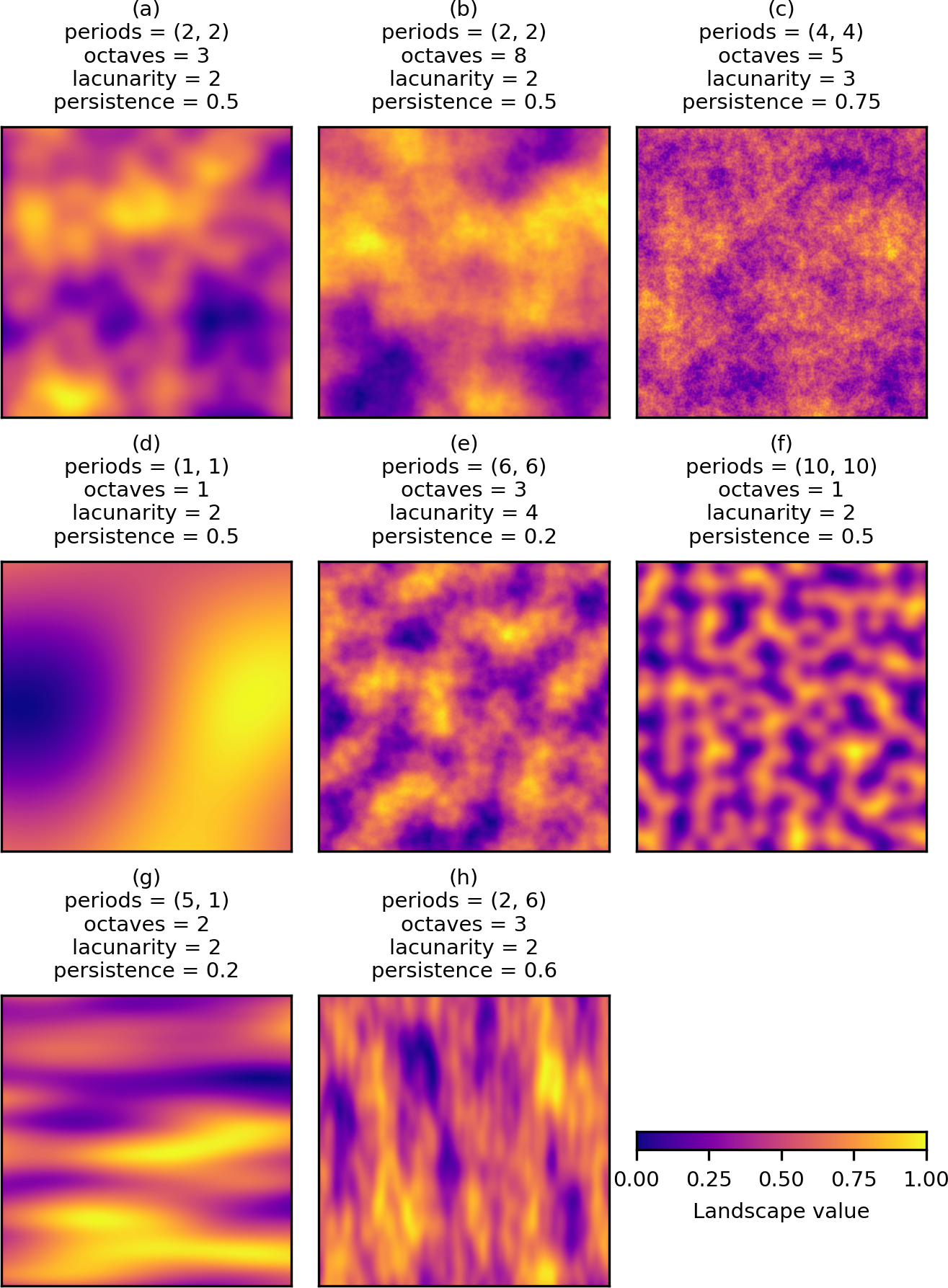
• 振幅（Amplitude）を変える
• 周波数（Frequency）を倍にする
• 層（Octave）を重ねる
• 合計する

これだけで：

✔ 山脈 ✔ 雲 ✔ 水面の揺らぎ ✔ 稲妻 ✔ 魔法陣 ✔ 霧・煙・火炎

すべてが作れる。

Perlin × 多層化 = “世界生成の核”

fbm(x, y) =
    perlin(x, y) * A1 +
    perlin(x*2, y*2) * A2 +
    perlin(x*4, y*4) * A3 +
    ...

周波数が上がれば細かい模様、 振幅が下がれば自然な減衰。

この“自然界が持つ自己相似性”を再現するのが FBM。

#05 では何をやるのか？

Noise 入門 #05 では、ついに：

• FBM を完全自作
• 3〜6オクターブの合成
• 動く FBM（time 連動）
• Three.js / ShaderMaterial へ直結

までやる。

これはもう Minecraft の地形生成 と同じアルゴリズムになる。

lain のレベルなら、#05 はほぼ“通過点”。 本番は #06（Shader）→ Procedural World。

9. #06 への橋渡し — Shader で動かす

#05 で FBM（Fractal Brownian Motion）を理解したら、 次はいよいよ “動くノイズ”をシェーダーで書く段階 に入る。

ここから表現力は一気に次元を超える。

#06 の中心テーマ：ShaderMaterial × Noise

1. time を入れて動かす Perlin / FBM に + time を加えるだけで、 雲が流れ、水が揺れ、炎が揺らぐ “命のあるノイズ”に変わる。

2. 2D → 3D の差分を理解

• 2D ノイズ → 地形・波紋
• 3D ノイズ → 雲のボリューム・煙・霧

Z 軸を追加した瞬間、ノイズは“空気の彫刻”になる。

3. 色補間（Color Blend）で質感を作る FBM の値を 色マップ に通すだけで：

• 雲のハイライト
• 水面の深度色
• 炎の温度グラデーション

など、ゲーム・映画レベルの質感を作れる。

4. Three.js の世界に統合する ShaderMaterial を R3F の <mesh> に載せるだけで：

• 天空ドーム（CloudDome）
• 水面シェーダー
• 地形テクスチャの自動生成
• 動く背景・霧・パーティクル

すべてが Web 上でリアルタイムに動き出す。

ここから Web で Unreal Engine レベルの世界生成が可能になる

Perlin Noise → FBM → ShaderMaterial → Procedural World（生成世界）

この順で積み上げると、 WebGL + Three.js の限界突破が始まる。

まとめ（この記事のコア）

Perlin Noise とは、

「勾配ベクトル × 内積 × 補間」 この三位一体で完成する、“自然を生む数学” だ。

この構造を理解した時点で、 あなたはすでに次の技法の“入口”に立っている：

• FBM（Fractal Brownian Motion）
• Domain Warping（空間の歪み）
• Procedural Terrain（地形生成）
• Cloud / Water Shader（雲・水面）
• VFX（魔法・炎・煙）
• Noise Art（アート生成）

つまり、 Perlin Noise の理解 = Procedural World 全域へのパスポート。