[Noise 入門 #02] ノイズを作る数学の基礎 — グリッド・勾配・補間を理解する

はじめに

Noise 入門 の第二回。

今回は、ノイズを作る数学の基礎を学習。

前回の記事：

ノイズを作る数学の土台 — グリッド・勾配・補間を理解する

この記事の目的:

「Perlin / Simplex を理解するための“最低限の数学”」を、
誰でも読めるレベルに分解して説明する。

前回の #01 は“ノイズとは何か？”という概念の話だった。
今回は ノイズを作る側の数学 を理解する。

この記事を読むと理解できること

  • ノイズの“素材”になる グリッド（格子）
  • なぜ 勾配ベクトル（gradient） が必要なのか
  • 自然の揺らぎに必須の 補間（interpolation）
  • ノイズにおける frequency / amplitude の意味
  • Value Noise と Perlin の違いが“一瞬で分かる”視点

1. すべてのノイズは《グリッド（格子）》から始まる

ノイズと言っても “ランダム値をただ並べたもの” ではない。 実際のノイズ生成は《格子状に区切られた空間》をベースにして構築される。

この格子（grid）は、数学的には 整数座標で区切られた空間 のこと。

ノイズを作るときに行うのは、たったの 2つだけ：

1. 各グリッド点に “値（Value）” を置く

これは Value Noise（バリューノイズ） の方式。

  • 各格子点に乱数値を置く
  • その値を補間して滑らかに見せる

値を置いて、補間でつなぐだけのシンプルな構造。

2. 各グリッド点に “方向ベクトル（Gradient）” を置く

こちらは Perlin Noise（パーリンノイズ） で使われる方式。

  • 格子点に小さな勾配ベクトル（方向ベクトル）を置く
  • ピクセルから格子点へのベクトルと 内積 をとる
  • それらを補間することでノイズを構成する

Value Noise と Perlin Noise の違いは“置くものだけ”

表現の複雑さに反して、根本の違いは驚くほど単純：

方式 格子点に置くもの
Value Noise 値（Value）
Perlin Noise 勾配ベクトル（Gradient）

つまり、ノイズの本質は「グリッドに何を置いて、どう補間するか」だけ で決まる。

2. Value Noise：まずは一番シンプルなノイズ

Value Noise は、ノイズの中で最もシンプルな方式。 「格子点に乱数を置き、その間を補間でつなぐ」だけ で滑らかなパターンが生まれる。

Value Noise の基本原理

  • 格子点：乱数（0〜1）を割り当てる
  • 格子点の間：補間（interpolation）で値を滑らかにつなぐ

つまり Value Noise とは：

「乱数 × 補間」＝ 滑らかな疑似乱数

という非常に単純な構造でできている。

Value Noise の処理の流れ

ノイズの計算は以下のように進む。

1. グリッド（整数座標）を求める

現在の座標 (x, y) が属する 左下の整数座標 (i, j) を求める。

i = floor(x)
j = floor(y)

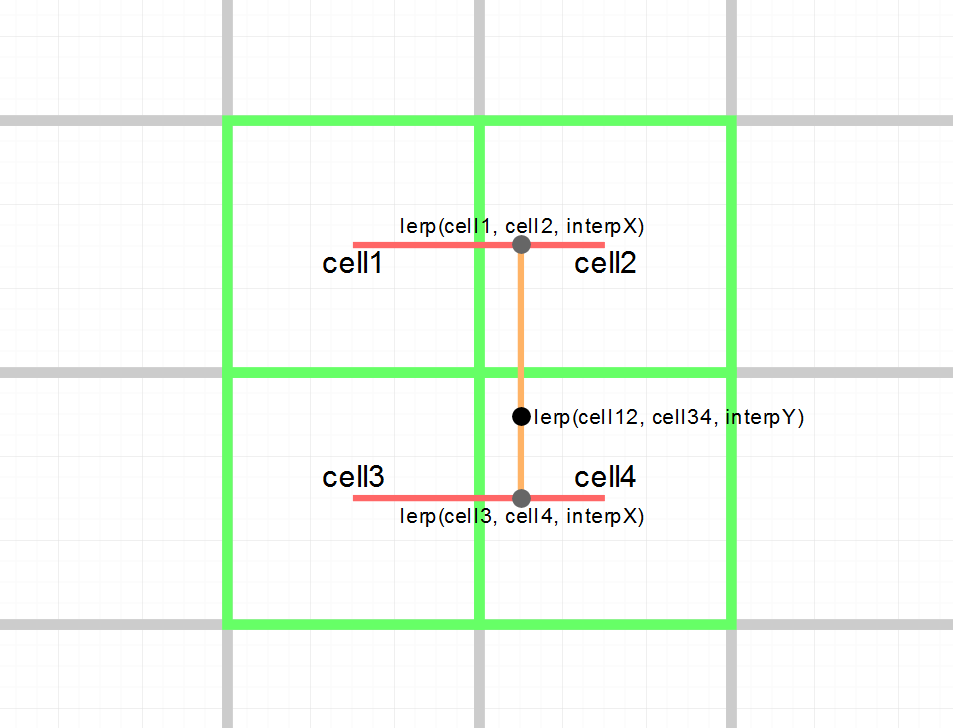
2. 周囲4点の値を取得する

Value Noise は 周囲の4点（2×2） を参照する。

v00 = value(i,   j)
v10 = value(i+1, j)
v01 = value(i,   j+1)
v11 = value(i+1, j+1)

3. 上下方向（Y方向）に補間する

縦方向に補間して、

a = lerp(v00, v01, fy)
b = lerp(v10, v11, fy)

fy = y - j は格子点からの相対位置（0〜1）。

4. 左右方向（X方向）に補間する

横方向にも補間して、最終値を得る。

noise = lerp(a, b, fx)

fx = x - i（横方向の相対位置）。

5. 結果として “滑らかなノイズ” が得られる

これが Value Noise の完成形。 非常にシンプルだが、後で出てくる

  • FBM（Fractal Brownian Motion）
  • Turbulence
  • Ridge Noise

など 全ての鍵となる基礎構造 になる。

Value Noise を理解すると、ノイズの“核”が掴める。

Value Noise が重要な理由

後の Perlin・Simplex がどれだけ複雑に見えても、 根本原理は 「周囲から値を取り、補間する」 という Value Noise と同じ。

つまり：

Value Noise を理解する = ノイズ全体系の基礎を手に入れる

この回はそのための最重要ステップ。

3. Perlin Noise：Value にベクトル（勾配）を導入したもの

Value Noise では「格子点に値を置いて補間」していた。
しかしこの方式では 格子っぽい縞（artifact）が残りやすい。

そこでケン・パーリンが発明したのが “勾配ベクトル（gradient vector）” を使う方式。

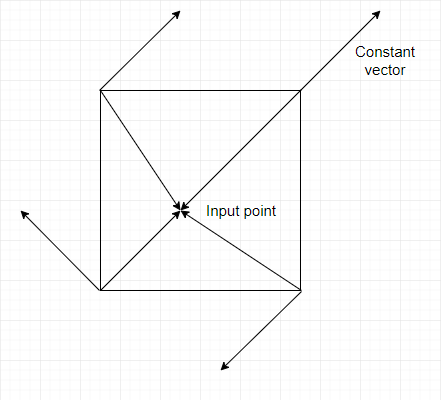
勾配ベクトルとは？

各グリッド点に置く “方向だけを持つベクトル” のこと。 大きさは 1（単位ベクトル）。

→   ↗   ↑   ↖
←   ↙   ↓   ↘

なぜ方向を置くのか？ 理由はシンプル：

方向ベクトル × 内積 = “滑らかさの源” を生むから。

Value Noise が「値の補間」だったのに対し、 Perlin Noise は「内積の補間」で表情が決まる。

Perlin Noise の計算手順（数学的に正しい流れ）

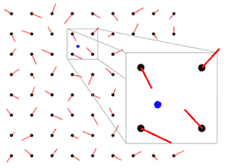
以下が1ピクセル（1座標）を求める処理：

1. 格子点の勾配ベクトルを取得する

g00 = gradient(i,   j)
g10 = gradient(i+1, j)
g01 = gradient(i,   j+1)
g11 = gradient(i+1, j+1)

勾配ベクトルは、あらかじめ決めた3〜8方向からランダムに選ぶ。

2. ピクセルから格子点へのベクトルを計算する

d00 = (fx,  fy)
d10 = (fx-1, fy)
d01 = (fx,  fy-1)
d11 = (fx-1, fy-1)

fx, fy はピクセルの“グリッド内での相対位置”（0〜1）。

3. 各格子点で《内積》をとる

n00 = dot(g00, d00)
n10 = dot(g10, d10)
n01 = dot(g01, d01)
n11 = dot(g11, d11)

この 内積（dot product） こそ Perlin の核心。

理由： “方向の一致度” を滑らかに変化させる計算だから。

4. 内積値を補間する → これが最終ノイズ値

まず上下で補間：

a = lerp(n00, n01, smooth(fy))
b = lerp(n10, n11, smooth(fy))

次に左右でも補間：

noise = lerp(a, b, smooth(fx))

Perlin では linear ではなく、 quintic（5次補間） を使うのが特徴。

Value と Perlin の違い（理解の核心）

要素 Value Noise Perlin Noise
格子点に置く 値（Value） 勾配ベクトル（Gradient）
計算の核 値の補間 内積の補間
見た目 やや格子感 最も自然で滑らか
計算の意味 ランダムの平滑化 方向性のある揺らぎ

Perlin で重要なのはただ1つ：

内積（方向 × 相対位置）を補間したものがノイズになる。

これで自然界の“揺らぎ”に近い変化が生まれる。

理解のポイント：本質はたった1行

noise(x) = interpolate( dot(gradient, direction) )

この1行の理解が Perlin → Simplex → Curl → FBM → Warping すべての基礎になる。

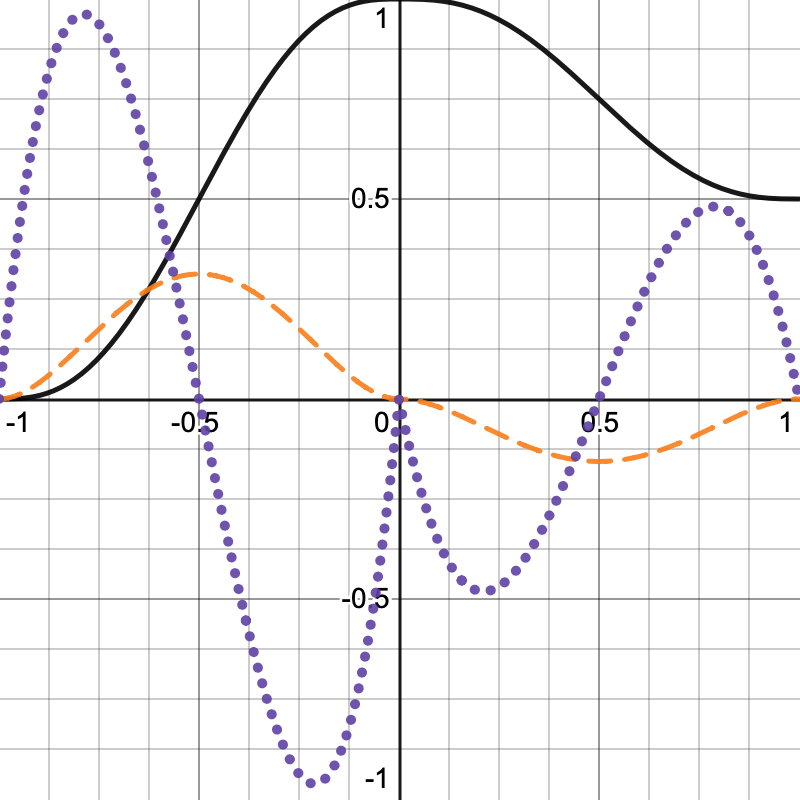
4. ノイズを“自然らしくする”のは《補間関数》

ノイズを自然に見せるために最も重要なのが 補間（interpolation） だ。
もし補間が線形（linear）のままだと、出てくる模様は 機械的で硬い縞（banding） になってしまう。

滑らかな自然模様を作るために、ノイズでは
smoothstep や quintic（5次補間） が使われる。

なぜ補間が必要なのか？

Value Noise・Perlin Noiseは、どちらも
周囲の格子点から値（Value または 内積スカラー）を補間して滑らかにする
という共通構造を持つ。

つまり、補間の質＝ノイズの品質。

線形補間（linear）だと何が起きる？

lerp(a, b, t) = a + (b - a) * t

線形補間は計算が最も簡単だが…

  • 変化が均一すぎる
  • 勾配の変化が急に切り替わる
  • 結果、ノイズに“人工的な縞”が出やすい

自然界の揺らぎとは程遠くなる。

smoothstep：自然の揺らぎに最初の一歩

smoothstep(t) = t * t * (3 - 2 * t)
  • 始まりと終わりの勾配が0になる（C¹連続）
  • 変化が自然に見える
  • グラデーションが柔らかくつながる

Perlin Noise の補間にも使われるが、最終的には quintic が推奨される。

quintic（5次補間）：Perlin が推奨する本命

quintic(t) = t^3 * (t * (t * 6 - 15) + 10)

ポイント：

  • 勾配がさらに滑らか（C²連続）
  • ノイズの継ぎ目が極端に目立たない
  • Perlin Noise を美しくする決定打

簡単に言うと：

smoothstep よりさらに“自然界の滑らかさ”に近づける補間

Perlin が自著で最終的に推したのも quintic。

よく使う補間の比較

名前 特徴
linear 最も簡単。縞が出やすい。
smoothstep 自然な感じ。C¹連続で綺麗。
quintic（推奨） さらに滑らか。Perlin 推奨の本命。

Perlin Noise が美しい理由

Perlin Noiseの滑らかさは
“勾配 × 内積 × 高品質の補間”
が組み合わさることで生まれる。

もし linear 補間を使ったら、Perlin でも縞が出る。
逆に、Quintic を使えば Value Noiseでもかなり綺麗になる。

つまり：

ノイズの本当の美しさを決めるのは “補間” である。

5. frequency（周波数）と amplitude（振幅）

ノイズの“見た目の粗さ”や“模様のスケール”は
frequency（周波数） によって劇的に変化する。

frequency（周波数）とは？

簡単に言うと：

ノイズの「細かさ」や「スケール」を決めるパラメータ。

周波数が低い（frequency が小さい）

  • 大きなうねり
  • なだらかで広域の模様
  • 風景・雲・地形の“全体形状”に向いている
~~~~~~    ← ゆっくり変化

周波数が高い（frequency が大きい）

  • 細かい模様が密集
  • シャープでザラついた構造
  • 砂・ノイズテクスチャ・火花などに向いている
^^^^^^^^  ← 細かい揺らぎ

振幅（amplitude）とは？

Amplitude は ノイズの“高さ（強度）” を決める。

  • amplitude が小さい → 弱い揺らぎ
  • amplitude が大きい → 激しい変化

周波数と amplitude は FBM（Fractal Brownian Motion） で特に重要になる。

FBM における frequency と amplitude の役割

FBM では 複数オクターブのノイズを重ねる。 その際、各オクターブで frequency と amplitude を変化させる。

例（典型）：

octave 1: frequency=1   amplitude=1
octave 2: frequency=2   amplitude=0.5
octave 3: frequency=4   amplitude=0.25
octave 4: frequency=8   amplitude=0.125

つまり：

  • frequency → 細かさを増やす
  • amplitude → 影響力を減らす

この “細かくしながら高さを下げる” という構造が
FBM の 自然なフラクタル表情 を生み出す。

まとめ：frequency と amplitude はノイズの“人格そのもの”

パラメータ 役割
frequency ノイズの細かさ・スケール
amplitude 揺らぎの強さ・高さ

両者が連動することで、
雲、山、炎、水、煙…あらゆる自然模様が作れる。

結論：

frequency = 大きさ、amplitude = 力強さ

この2つはノイズの“人格”を決める最重要パラメータ。

6. Value と Perlin の違いを“一撃で理解”するまとめ

Value Noise と Perlin Noise の違いは複雑に見えて、 本質的には 「格子点に何を置いて、何を補間するか」 の2点しか違わない。

違いが一瞬で分かる比較表

項目 Value Noise Perlin Noise
格子点に置くもの 乱数の“値”（Value） 単位ベクトル（Gradient）
計算の核 値を補間する 内積（direction × gradient）を補間
見た目 ほんのり格子感が残る より自然・滑らかで連続的
実用 地形、標高マップ、粗いパターン 雲・水・炎・煙・地形・VFX すべてに対応

理解の“核心”はこの一行

Value Noise  = 値の補間
Perlin Noise = 内積の補間（方向性のある揺らぎ）

これだけで、 なぜ Perlin が自然で、Value が少し人工的になるのか が説明できる。

ここで得るもの

  • Value = ノイズの“原点”
  • Perlin = 自然界のゆらぎに近づける“改良版”
  • 違いは概念的にはシンプルだが、見た目の差は大きい
  • 後の FBM, Simplex, Curl, Domain Warping の理解が一気に楽になる

このセクションで ノイズの基礎2種類を完全に把握 できる。

7. まとめ

ノイズ生成は一見すると難しそうに見えるが、
実際の本質は驚くほどシンプルだ。

ここまで理解した段階で、いよいよ——

  • Perlin Noise（勾配ノイズの基本形）
  • Simplex Noise（次世代の改良版ノイズ）
  • FBM（Fractal Brownian Motion）
  • Domain Warping（神領域の歪曲ノイズ）

これら“本格的なノイズ技法”に進む 入口 に立てる。

ノイズが難しく見える理由

名称やアルゴリズムが増えていくため、どうしても複雑に見える。

しかし 核になっている数学はたった3つ しかない。

ベクトル（方向）
内積（方向の一致度を測る）
補間（滑らかにつなぐ）

たったこれだけで、
雲・炎・水・煙・地形・魔法陣・宇宙エフェクト……
あらゆる“自然のゆらぎ”が作れる。