[数学] 線形代数 第4回: 線形変換と固有値 座標系の変換から物体の挙動解析まで、線形変換と固有値の応用

線形変換（Linear Transformation）

定義と基本性質

• 線形変換は、二つのベクトル空間 (V) と (W) （同じ体 (\mathbb F) 上）に対して、写像

が以下の二条件を満たすときに「線形」であると言います：

1. 加法保存：

$$ T(\mathbf u + \mathbf v) = T(\mathbf u) + T(\mathbf v)　 $$

for all　$$ (\mathbf u, \mathbf v \in V)$$　. (Lafayette Sites)　

1. スカラー倍保存： $$ T(c \mathbf u) = c,T(\mathbf u)　$$ for all scalar $$(c\in\mathbb F)$$ and $$(\mathbf u \in V)$$ (Lafayette Sites)

• この定義から次のことが導かれます：

  • $$(T(\mathbf 0_V) = \mathbf 0_W)$$.（零ベクトルが零へ写る） (ウィキペディア)

  • 線形変換は、ベクトル空間の構造（線形結合など）を保つ性質があるため、多くの応用で “変換” を表現する道具として使われます。 (DeepAI)

• ベクトル空間とは何か、という基本も押さえておくと良いです。たとえば、ベクトルの加法・スカラー倍が定義された集合で、いくつかの公理を満たします。 (ウィキペディア)

行列による表現

• 有限次元のベクトル空間 $$(V\cong \mathbb F^n)$$、$$(W\cong \mathbb F^m)$$ の場合、基底を選ぶと線形変換 $$(T: V \to W)$$ は 行列 (A) によって表せます。つまり、ある基底でのベクトル $$(\mathbf x)$$ の座標を掛けることで $$(T(\mathbf x))$$ の座標が得られます。 (バークレー大学数学科)

• 例えば、2D空間での拡大・回転・反射などは対応する2×2行列によって表せます。

• この「基底を変える（＝座標変換）と行列が変わる」という点も重要：基底を変えれば行列も似行列$$（(B^{-1}AB) 型）$$になります。 (ウィキペディア)

幾何学的イメージとゲーム開発への関係

• 幾何学的には、線形変換とは「原点を含む直線・平面を別の直線・平面に写す」操作です。例えば、2Dでベクトルを回転させる・拡大する・せん断（シアー）させるようなもの。

• ゲーム／グラフィックス開発では、次のような場面で活用されます：

  • キャラクターやエフェクトの座標をワールド座標→カメラ座標へ変換（ビュー・プロジェクション変換）
  • オブジェクトの拡大・縮小（スケーリング）、回転、反転
  • 物理的な変換（例えば剛体の回転）や、メッシュ／モデルの変形

• また、2D・3Dのアニメーションやエフェクトで「時系列的に位置や向きが変化する」際、線形変換を逐次適用すると効率的です。たとえば「星がキラキラ乱舞する」ようなアニメーションで、座標＋回転＋拡大を組み合わせて表現できます。

• ゲームロジックや演出において「このベクトルはこの変換を受けたらどうなるか」を予測する力が、線形変換の理解で格段に上がります。

深堀すべき観点

以下の観点を深く掘っていくことで、理論だけでなく実装／表現力も強化できます：

1. 核 (kernel) と像 (image／range)

   • 線形変換$$ (T: V\to W) $$に対して、$$(\ker T = {v \in V \mid T(v)=0})$$、$$(\operatorname{im}T = {T(v)\mid v\in V})$$ はそれぞれベクトル空間です。 (Brilliant)
   • ゲームで考えると、「この変換で消える方向（変化しない／無効化されるベクトル）」「この変換で得られる範囲（実際に移動・変形される方向）」を把握することが、最適化・バグ防止につながります。

2. 基底・次元・変換の可逆性

   • 行列（変換）が可逆である → 逆変換が存在。これは $$(\det A \neq 0)$$ のとき。基底の選び方・次元の扱いが関わります。 (ウィキペディア)
   • ゲーム開発では、「ある座標系へ移した後に戻す」処理や、「オブジェクトの親子変換（ワールド→ローカル→ワールド）」などで逆変換が出てきます。

3. 座標変換・基底変換

   • ある基底で表現した行列を、別の基底に移すことで形が変わります。基底が変わると座標上での「見え方」も変わります。 (ウィキペディア)
   • ゲームで言えば、「オブジェクト空間 → ワールド空間 → カメラ空間」といった複数の座標系を行き来する処理が必要になるため、この基底変換の理論を知っておくと設計が楽です。

4. 特殊な線形変換タイプ

   • 反射、回転、せん断（シアー）、投影（プロジェクション）など。例えば、投影行列は$$ (P^2 = P) $$を満たすものがあります。 (ウィキペディア)
   • ゲームの演出で「影を落とす」「カメラの平面に投影する」「UIの2D座標変換を3D空間上で行う」などに応用できます。

5. 変換の合成・順序

   • ２つ以上の線形変換を続けて適用すること（合成）は、新しい線形変換になります。行列で言えば、$$(T_1\circ T_2)$$ に対応するのは行列積 $$(A_1 A_2)$$
   • 実装上、効率よくまとめて変換を行う際、この性質を活用できます（例えば、世界変換＋ビュー変換を一つの行列に纏める）。

次ステップとして取り扱う内容

• 行列の 固有値・固有ベクトル とその幾何学的意味、変換の分解（対角化、ジョルダン標準形）
• 変換を視覚的に表現する（2D／3D回転マトリクス、スケーリングマトリクス）および実装コード（例えば JavaScript＋Canvas／WebGL）とのリンク
• ゲーム的に「線形変換を演出として使う」パターン（例：背景スケールで奥行きを出す、回転インパクト演出、せん断でスピード感を出す）
• 計算パフォーマンス・精度の観点（浮動小数点誤差、行列積の最適化、変換順序の最適化）

このように「線形変換」の理論を、あなたが持つ描画／アニメーションスキル、ゲーム表現への意識とリンクさせて掘ることで、単なる数学知識以上の“表現力”を得られます。

回転・拡大縮小・せん断を行列として実装する

回転、拡大縮小、せん断（シアー）の線形変換を行列で表現し、JavaScriptを使って実装する方法を説明します。

1. 回転行列（Rotation Matrix）

2D空間での回転を表現する行列です。回転角度を (\theta) とすると、回転行列は次のように表されます。

$$ R(\theta) = \begin{pmatrix} \cos\theta & -\sin\theta \\ \sin\theta & \cos\theta \end{pmatrix} $$

この行列を2Dベクトル $$ \mathbf{v} = \begin{pmatrix} x \\ y \end{pmatrix}$$ に掛けることで、ベクトルが (\theta) 度回転します。

実装例 (JavaScript)

// 回転行列を作成する関数
function rotationMatrix(angle) {
    const radians = angle * Math.PI / 180; // 度をラジアンに変換
    return [
        [Math.cos(radians), -Math.sin(radians)],
        [Math.sin(radians), Math.cos(radians)]
    ];
}

// ベクトルと行列を掛け合わせる関数
function multiplyMatrixAndVector(matrix, vector) {
    return [
        matrix[0][0] * vector[0] + matrix[0][1] * vector[1],
        matrix[1][0] * vector[0] + matrix[1][1] * vector[1]
    ];
}

// 使用例: (1, 0) のベクトルを 90 度回転
const angle = 90;
const vector = [1, 0];
const matrix = rotationMatrix(angle);
const rotatedVector = multiplyMatrixAndVector(matrix, vector);

console.log(rotatedVector);  // 結果: [0, 1]

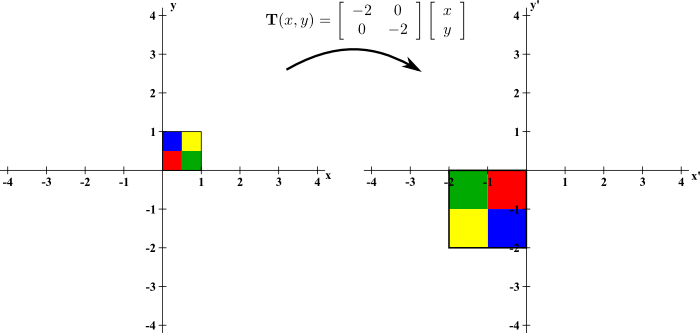
2. 拡大縮小行列（Scaling Matrix）

拡大縮小を行う行列です。スケール因子 (sx) と (sy) を用いて、次のように表されます。

$$ S(sx, sy) = \begin{pmatrix} sx & 0 \\ 0 & sy \end{pmatrix} $$

この行列をベクトルに掛けることで、ベクトルの各成分がそれぞれスケーリングされます。

実装例 (JavaScript)

// 拡大縮小行列を作成する関数
function scalingMatrix(sx, sy) {
    return [
        [sx, 0],
        [0, sy]
    ];
}

// 使用例: (1, 1) のベクトルを 2倍に拡大
const scaleX = 2;
const scaleY = 2;
const vector2 = [1, 1];
const scaleMatrix = scalingMatrix(scaleX, scaleY);
const scaledVector = multiplyMatrixAndVector(scaleMatrix, vector2);

console.log(scaledVector);  // 結果: [2, 2]

3. せん断行列（Shearing Matrix）

せん断（シアー）は、座標軸に沿ってベクトルを歪める操作です。例えば、x軸方向にせん断する行列は次のように表されます。

$$ H_x(k) = \begin{pmatrix} 1 & k \\ 0 & 1 \end{pmatrix} $$

ここで (k) はせん断係数です。同様に、y軸方向にせん断する行列は次のように表されます。

$$ H_y(k) = \begin{pmatrix} 1 & 0 \\ k & 1 \end{pmatrix} $$

実装例 (JavaScript)

// せん断行列を作成する関数
function shearingMatrix(kx, ky) {
    return [
        [1, kx],
        [ky, 1]
    ];
}

// 使用例: (1, 1) のベクトルに x 軸方向に 2 倍のせん断を適用
const shearX = 2;
const shearY = 0;
const vector3 = [1, 1];
const shearMatrix = shearingMatrix(shearX, shearY);
const shearedVector = multiplyMatrixAndVector(shearMatrix, vector3);

console.log(shearedVector);  // 結果: [3, 1]

線形変換を使ったアニメーション

これらの行列を使用して、ゲーム内のオブジェクトを変換する際にアニメーション効果を加えることができます。例えば、回転しながら拡大縮小を行ったり、せん断でエフェクトを変化させたりすることが可能です。

アニメーション例 (JavaScript Canvas)

// キャンバスと描画
const canvas = document.getElementById('myCanvas');
const ctx = canvas.getContext('2d');

// アニメーションの設定
let angle = 0;
let scaleX = 1, scaleY = 1;
let shearX = 0.2;

function draw() {
    ctx.clearRect(0, 0, canvas.width, canvas.height);

    // 回転行列、拡大縮小行列、せん断行列を組み合わせる
    const rotation = rotationMatrix(angle);
    const scale = scalingMatrix(scaleX, scaleY);
    const shear = shearingMatrix(shearX, 0);

    const transformationMatrix = multiplyMatrixAndVector(rotation, [scale[0][0], scale[1][0]]);
    const finalTransform = multiplyMatrixAndVector(shear, transformationMatrix);

    // 描画: 正方形を変換
    ctx.save();
    ctx.setTransform(finalTransform[0], finalTransform[1], finalTransform[1], finalTransform[0], canvas.width / 2, canvas.height / 2);
    ctx.fillStyle = 'blue';
    ctx.fillRect(-50, -50, 100, 100);
    ctx.restore();

    // アニメーション進行
    angle += 1;
    scaleX = 1 + Math.sin(angle * Math.PI / 180) * 0.5;  // スケールを変化させる
    shearX = Math.sin(angle * Math.PI / 180) * 0.2;  // せん断効果を変化

    requestAnimationFrame(draw);
}

draw();

まとめ

• 回転行列は物体の回転に使用されます。
• 拡大縮小行列は物体のサイズを変更するために使用します。
• せん断行列は物体を歪ませるために使います。
• JavaScriptとCanvasを使ってこれらの行列を適用し、リアルタイムでオブジェクトを変換するアニメーションを作成できます。

この方法を使うと、ゲームやアプリの中で動的に物体を変換することができ、表現の幅が広がります。

固有値と固有ベクトル

では、固有値と固有ベクトルについて深掘りしていきましょう。

固有値と固有ベクトルの定義

固有ベクトル (Eigenvector)

線形変換 ( T ) において、あるベクトル ( \mathbf{v} ) が、変換後に方向を変えずにスカラー倍されるような特別なベクトルを「固有ベクトル」と呼びます。具体的には、次の条件を満たすベクトル ( \mathbf{v} ) を言います。

$$T(\mathbf{v}) = \lambda \mathbf{v}$$

ここで、( T ) は線形変換、( $$\mathbf{v}$$ ) は固有ベクトル、( $$\lambda$$ ) はスカラー（固有値）です。固有ベクトルは線形変換により方向を変えず、サイズのみがスケールされます。

固有値 (Eigenvalue)

固有値は、その固有ベクトルに対応するスカラー量です。線形変換 ( T ) が固有ベクトルに作用することで、ベクトルの大きさがどの程度拡大・縮小されるかを表します。つまり、固有値$$ \lambda $$ は、対応する固有ベクトルがスケーリングされる「倍率」を示します。

固有値と固有ベクトルの計算方法

固有値と固有ベクトルは、行列 ( A ) に対して次の特性方程式を使って求めます：

$$ A \mathbf{v} = \lambda \mathbf{v} $$

この式を $$ A \mathbf{v} - \lambda \mathbf{v} = 0 $$ と書き換え、行列式を使って以下のように求めます：

$$ (A - \lambda I) \mathbf{v} = 0 $$

ここで、( I ) は単位行列で、行列 $$ (A - \lambda I) $$ の行列式 $$ \text{det}(A - \lambda I) = 0 $$ を解くことで、固有値 $$ \lambda $$ を求めます。

その後、固有値 $$ \lambda $$ を代入して対応する固有ベクトル $$ \mathbf{v} $$ を求めます。

固有値と固有ベクトルの計算例

例1: 2x2 行列

行列 ( A ) が次のように与えられているとしましょう：

$$ A = \begin{pmatrix} 4 & 1 \ 2 & 3 \end{pmatrix} $$

この行列の固有値と固有ベクトルを求めます。

1. 特性方程式を立てる

まず、特性方程式を解くために、行列 ( A ) と固有値 ( \lambda ) を使って次の式を立てます：

$$ \text{det}(A - \lambda I) = 0 $$

$$ A - \lambda I = \begin{pmatrix} 4 - \lambda & 1 \ 2 & 3 - \lambda \end{pmatrix}$$

行列式を計算します：

$$\text{det}(A - \lambda I) = (4 - \lambda)(3 - \lambda) - 2 \times 1$$

$$\text{det}(A - \lambda I) = (4 - \lambda)(3 - \lambda) - 2 = 12 - 7\lambda + \lambda^2 - 2$$

$$\text{det}(A - \lambda I) = \lambda^2 - 7\lambda + 10 = 0$$

2. 固有値 ( \lambda ) を求める

この二次方程式を解きます：

$$\lambda^2 - 7\lambda + 10 = 0$$

解の公式を使うと：

$$ \lambda = \frac{-(-7) \pm \sqrt{(-7)^2 - 4(1)(10)}}{2(1)} = \frac{7 \pm \sqrt{49 - 40}}{2} = \frac{7 \pm \sqrt{9}}{2} = \frac{7 \pm 3}{2}$$

よって、固有値は次の2つです：

$$ \lambda_1 = 5, \quad \lambda_2 = 2 $$

3. 固有ベクトルを求める

それぞれの固有値について固有ベクトルを求めます。

• 固有値 $$\lambda_1 = 5$$ の場合、行列 $$ (A - 5I) $$ を使って固有ベクトル $$ \mathbf{v_1} $$ を求めます：

$$ A - 5I = \begin{pmatrix} 4 - 5 & 1 \\ 2 & 3 - 5 \end{pmatrix} = \begin{pmatrix} -1 & 1 \\ 2 & -2 \end{pmatrix}$$

この行列に対して ( (A - 5I) \mathbf{v_1} = 0 ) を解くと、固有ベクトルは次のようになります：

$$ \mathbf{v_1} = \begin{pmatrix} 1 \\ 2 \end{pmatrix} $$

• 固有値 ( \lambda_2 = 2 ) の場合、行列 ( (A - 2I) ) を使って固有ベクトル ( \mathbf{v_2} ) を求めます：

$$ A - 2I = \begin{pmatrix} 4 - 2 & 1 \\ 2 & 3 - 2 \end{pmatrix} = \begin{pmatrix} 2 & 1 \\ 2 & 1 \end{pmatrix} $$

この行列に対して ( (A - 2I) \mathbf{v_2} = 0 ) を解くと、固有ベクトルは次のようになります：

$$ \mathbf{v_2} = \begin{pmatrix} -1 \\ 2 \end{pmatrix} $$

固有値と固有ベクトルのゲームやシミュレーションへの応用

固有値と固有ベクトルは、以下のようにゲームやシミュレーションで利用されます：

1. 物理エンジン：

   • 物体の動きの解析において、固有ベクトルは物体の主軸方向を示し、固有値はその方向におけるスケール（圧縮や拡大）を示します。特に、振動のモード（固有振動数）を計算する際に固有値を利用します。

2. 3D変換とアニメーション：

   • 3D空間での回転やスケーリングを行う際、行列を対角化することで計算が効率化できます。固有値は変換の影響を受ける軸方向を示し、固有ベクトルはその方向を示します。

3. データ圧縮：

   • 主成分分析（PCA）などのデータ解析手法では、データの固有ベクトルを使って高次元空間を低次元に圧縮するための最適な方向を求めます。

実装例: 固有値と固有ベクトルの計算（JavaScript）

以下は、2x2 行列に対して固有値と固有ベクトルを計算する簡単な例です。

// 行列式を計算する関数
function determinant(matrix) {
    return matrix[0][0] * matrix[1][1] - matrix[0][1] * matrix[1][0];
}

// 固有値を計算する関数
function calculateEigenvalues(matrix) {
    const a = matrix[0][0];
    const b = matrix[0][1];
    const c = matrix[1][0];
    const d = matrix[1][1];

    const trace = a + d;
    const det = determinant(matrix);

    const discriminant = Math.pow(trace, 2) - 4 * det;
    if (discriminant < 0) {
        return null; // 実数解がない場合
    }

    const lambda1 = (trace + Math.sqrt(discriminant)) / 2;
    const lambda2 = (trace - Math.sqrt(discriminant)) / 2;

    return [lambda1, lambda2];
}

// 固有ベクトルを計算する関数
function calculateEigenvector(matrix, lambda) {
    const a = matrix[0][0] - lambda;
    const b = matrix[0][1];
    const c = matrix[1][0];
    const d = matrix[1][1] - lambda;

    // 固有ベクトルは一意ではなく、スカラー倍可能
    // この例では、c = -bであることから、簡単に解を得られる場合を示します
    return [b, a];
}

// 使用例
const matrix = [[4, 1], [2, 3]];
const eigenvalues = calculateEigenvalues(matrix);
const eigenvector1 = calculateEigenvector(matrix, eigenvalues[0]);
const eigenvector2 = calculateEigenvector(matrix, eigenvalues[1]);

console.log('Eigenvalues:', eigenvalues);
console.log('Eigenvector 1:', eigenvector1);
console.log('Eigenvector 2:', eigenvector2);

まとめ

• 固有値と固有ベクトルは線形変換の重要な特性を示します。
• 固有値は変換におけるスケーリングの倍率、固有ベクトルはその方向を示します。
• ゲーム開発や物理シミュレーション、データ解析などで重要な役割を果たします。
• JavaScriptで固有値と固有ベクトルを計算する方法を紹介しました。

このように、固有値と固有ベクトルの理解は、ゲーム開発やシミュレーション、データ解析において非常に有用です。