【アルゴリズム入門】エラトステネスの篩とは？素数の見つけ方とBASIC実装まで（WebMSX）

はじめに

どんなきっかけか忘れましたが、Youtube動画のおすすめに、清水亮さんの動画が出て興味深かったので、記事にしてみました。

ハッカー魂 アルゴリズムの基本を文系にもわかるように解説した

動画の中で語られていますが、清水さんが学生時代に数学の授業で素数を提出する課題があり、パソコンを使ってもいいという条件があってその場合、１万個以下まで提出するのが条件だとか。

そこで利用したのが「エラトステネスの篩」というアルゴリズムで、当時はBASIC言語で答えを求めたとの事で、それに誘発されて、MSX BASICの動くWebMSXで動かしてみました。

🏺紀元前から続く数の冒険

「エラトステネスの篩（ふるい）」という名前を聞いたことがありますか？ このアルゴリズムは、紀元前3世紀のギリシャの学者エラトステネスによって考案されました。 「素数をどうやって見つけるか？」という、シンプルで奥深い問いに対する最古級のアルゴリズムです。

💡 素数とは？

まず、素数（prime number）とは何かを簡単におさらいしましょう。

素数とは、「1と自分自身」以外に約数を持たない、1より大きな自然数のこと。

例：

  • 2, 3, 5, 7, 11, 13, … は素数。
  • 4（=2×2）、6（=2×3）、9（=3×3）などは合成数（複数の因数を持つ）です。

🧠 エラトステネスの篩とは？

エラトステネスの篩は、合成数をふるい落とすことで素数だけを残す、非常に効率的なアルゴリズムです。

手順（100までの素数を求める例）：

  1. 2 〜 100 の数をすべて並べる。
  2. 2は素数なので残す。2の倍数をすべて消す。
  3. 次に残った3も素数。3の倍数をすべて消す。
  4. 次に残った5も素数。5の倍数をすべて消す。
  5. √100 ≒ 10 まで繰り返す。
  6. 残った数がすべて素数。

まるで「ザルで余分な数を落とす」ような動き。 このアルゴリズムが“篩（ふるい）”と呼ばれる理由です。

📜 BASICでの実装（MSX風）

10 DIM P(10000)
20 FOR I=2 TO 10000: P(I)=1: NEXT I
30 FOR I=2 TO 100
40   IF P(I)=1 THEN GOSUB 1000
50 NEXT I
60 FOR I=2 TO 10000
70   IF P(I)=1 THEN PRINT I
80 NEXT I
90 END

1000 FOR J=I*2 TO 10000 STEP I
1010   P(J)=0
1020 NEXT J
1030 RETURN
  • P(I)=1 は「素数の可能性あり」を意味します。
  • 倍数を 0 にして「合成数」として消していきます。

✅ WebMSXなどで動かせば、実際に素数一覧を高速で出力してくれます。

スクロールする数の美しさに、思わず息を呑むはず。

実際動かしてみましたが、１万だとアウトオブレンジになったので、実機では厳しそうです。 なので、１０００にしました。

エラトステネスの篩をMSX BASICで実装

🌐 JavaScriptでの実装

function sieve(n) {
  const prime = Array(n + 1).fill(true);
  prime[0] = prime[1] = false;

  for (let i = 2; i * i <= n; i++) {
    if (prime[i]) {
      for (let j = i * 2; j <= n; j += i) {
        prime[j] = false;
      }
    }
  }

  return prime.map((v, i) => v ? i : null).filter(v => v);
}

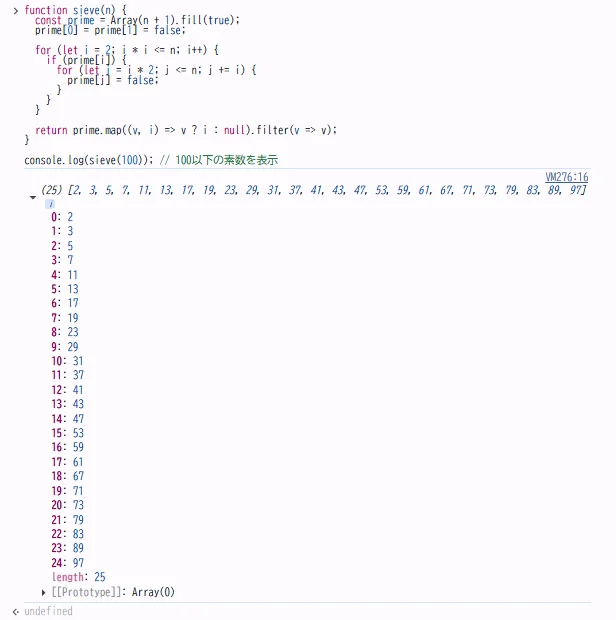
console.log(sieve(100)); // 100以下の素数を表示

BASICよりも短く、読みやすいコードで同じ処理を実現しています。


🧬 現代でも使われているの？

エラトステネスの篩は、現在でも十分に高速で簡潔な素数探索法として知られています。 大きな数まで求める際は「メモリ効率を改善した高速なバリエーション」も登場しています（例えば：Segmented Sieve や Bit Sieve）。

現代のRSA暗号などでも素数は重要な役割を持ち、篩の考え方は基礎技術として活きています。

✨ 感動する数学の瞬間

あなたは、教室で1人、問題が「解けてしまう」ことに感動した経験はありませんか？ 公式を使えば難問がスッと解ける。 それは、まるで暗闇で見つけた一筋の光のような瞬間です。

エラトステネスの篩も、そうした“感動”を今なお与えてくれるアルゴリズムのひとつです。

📝 まとめ

項目 内容
発案者 エラトステネス（紀元前3世紀）
アルゴリズム 合成数を除外して素数を見つける
実装例 BASIC（WebMSX）、JavaScript
応用例 素数探索、暗号、数学教育

📎 リンクと参考資料

✍️ おわりに

エラトステネスの篩は、古代から現代まで「シンプルな美しさ」と「応用力」を兼ね備えた傑作です。 このアルゴリズムを知った瞬間、あなたの中の“数学する心”が、またひとつ目を覚ますかもしれません。

関連リンク