
1. セグメントツリーって何?🌳
セグメントツリーとは、配列の特定の区間(range)に対する集約処理(集計)を高速に行うためのデータ構造です。
たとえば、次のような場面を考えてみてください:
📦 「配列の1〜5番目の中で、最大値を求めたい」 🧮 「毎回ループして数えると時間がかかる…もっと速くできない?」
このような問題に対して、セグメントツリーは「事前に処理結果を木構造にしておく」というアイデアで高速化を図ります。
🌲 木構造としての仕組み
- 元の配列を二分木に変換し、葉ノードに元の値を保持。
- 内部ノードには、それぞれ左右の子の集約結果(例:最大値、合計、論理ORなど)を格納。
- 上から順に結果が計算されるので、任意の区間の結果も対数時間(O(log N))で計算できる。
🧠 AIに聞いた例え話
「セグメントツリーは、大量のデータのサマリーを、木にしてストックしておく仕組みです。 必要な部分だけをうまく取り出して、全体を見なくても結果が分かるようになっています。」
📌 用途例
- 区間の最大値・最小値・合計を高速に取得
- 文字列内の種類数を判定(a〜z など)
- ゲームやグラフ構造での範囲クエリ対応
🔧 図の内容案(例:長さ8の配列 [5, 3, 7, 9, 6, 2, 1, 4] の最大値を扱うセグメントツリー)
- 葉ノード(最下段)に元の配列の値
- 内部ノードには左右の子の最大値
- 全体で1本の完全二分木
- 各ノードに値(例:最大値)を表示
構成イメージ:
[9]
/ \
[9] [6]
/ \ / \
[7] [9] [6] [4]
/ \ / \ / \ / \
[5][3][7][9][6][2][1][4]
このような構造を画像化して提供可能です。
🎨 質問:図のスタイルはどうしましょう?
以下から選んでも、こちらで提案してもOKです。
- 手書き風(参考書みたいな温かい雰囲気)
- クリアなデジタル図(白背景・シャープな線・色分けあり)
- ダーク背景でコードっぽく(ブログに馴染むかも)
また、どの演算を扱うかによって中身の値が変わります:
- 最大値(
max) - 合計(
sum) - 論理演算(例:bitのOR)
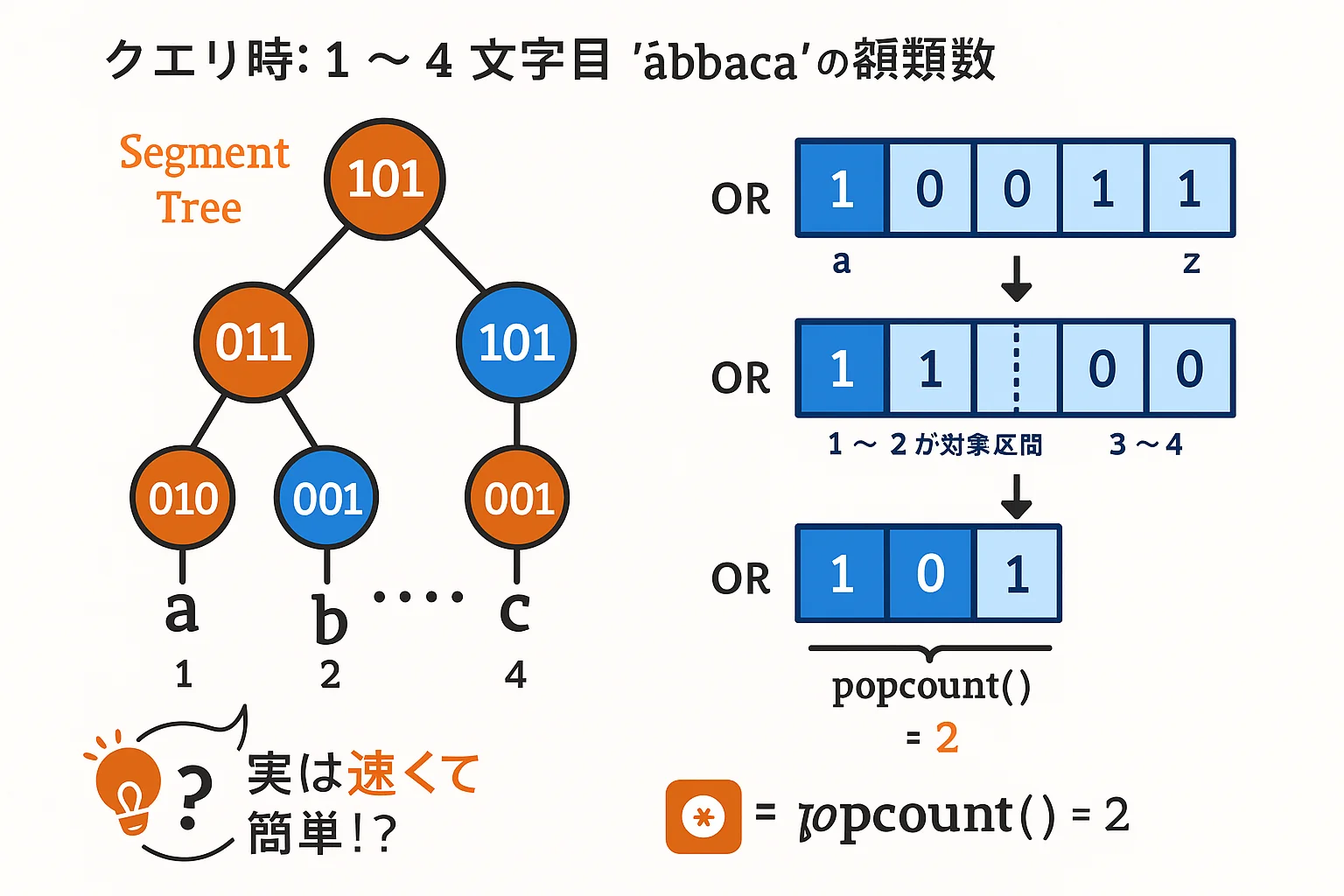
2. 実際の使用例:文字の種類数を数える場合
競技プログラミングでは「区間に含まれる文字の種類数」を高速に求める問題がよく登場します。
たとえば、文字列 "abbaca" があるとして、
- 区間
[1, 4]に含まれる文字の種類は? →"bba"→ 文字種は"a"と"b"→ 2種類
🧠 アプローチ:各文字をビットで管理!
26文字(a〜z)をそれぞれ 1ビット で表現します:
| 文字 | ビット表現 |
|---|---|
a |
000...0001 (bit 0) |
b |
000...0010 (bit 1) |
c |
000...0100 (bit 2) |
| … | … |
z |
100...0000 (bit 25) |
こうすることで、文字の存在情報を 1つの int 型(または uint32 など)で扱うことができます。
⚙ 区間の統合は OR 演算!
セグメントツリーの内部ノードには、「その区間で存在する文字のビット論理和」を持たせます。
"a"→0001"b"→0010"a" + "b"→0011
このように、複数文字があっても OR をとることで「その区間に何の文字が含まれているか」が一目で分かります。
🔍 popcount() を使えば種類数も一発!
得られたビット列に対して 1が何個立っているかを数えることで、種類数を求められます。
int kinds = __builtin_popcount(bitmask);
💡 AIの補足:「カウントではなく存在管理にすることで高速化できる」
1文字ずつ数えていたら O(n) ですが、ビット管理なら
- OR演算:高速
- popcount:1命令で完結
→ 全体で O(log n) で答えられる!
3. セグメントツリーの構築とクエリ処理
ここでは、文字列に基づいた「ビット管理によるセグメントツリー」の実装方針を、構築と**クエリ処理(区間の種類数取得)**に分けて解説します。
🏗️ 1. 構築:各文字をビット化して木を作る
まずは、1文字ずつ**ビット列(bitmask)**に変換します。
// 文字 'a'〜'z' → ビット 0〜25 に対応
int charToBit(char c) {
return 1 << (c - 'a');
}
これを葉ノード(セグメントツリーの末端)にセットして、内部ノードは OR 演算で上に伝搬します。
void build(const string &s) {
for (int i = 0; i < n; ++i)
seg[i + size] = charToBit(s[i]); // 葉にセット
for (int i = size - 1; i >= 1; --i)
seg[i] = seg[2*i] | seg[2*i+1]; // 子ノードのOR
}
ℹ️
segはセグメントツリーを格納する配列、sizeは2べきサイズです。
🔍 2. クエリ処理:区間に含まれる種類数を取得
[l, r) の区間に含まれる 全文字のビット論理和 を求めます。
int query(int l, int r) {
l += size;
r += size;
int res = 0;
while (l < r) {
if (l & 1) res |= seg[l++];
if (r & 1) res |= seg[--r];
l >>= 1;
r >>= 1;
}
return __builtin_popcount(res); // 種類数
}
✅ 使用例:
string s = "abbaca";
build(s);
cout << query(1, 4) << endl; // "bba" → 種類数 = 2("a", "b")
🧠 ポイント
| 処理 | 時間計算量 |
|---|---|
| 構築 | O(n) |
| クエリ処理 | O(log n) |
🍀 ビットによる高速管理とセグメントツリーによる効率的な集約が合わさって、非常に強力!
4. 🔁 更新処理:1文字の差し替えも O(log N)
セグメントツリーでは、1文字の更新も 上へ伝播するだけなのでとても効率的です。
✏️ 1. 差し替えの例:文字列中の s[i] を ‘x’ に変更
void update(int i, char c) {
i += size;
seg[i] = charToBit(c); // ビットを書き換え
// 親へ伝播
while (i > 1) {
i >>= 1;
seg[i] = seg[i*2] | seg[i*2+1];
}
}
✅ 使用例
string s = "abbaca";
build(s);
update(2, 'z'); // "abbaca" → "abzaca"
cout << query(1, 4) << endl; // "bza" → 種類数 = 3("a", "b", "z")
🧠 補足ポイント
O(log N)で任意の1文字を更新可能。- 差し替え後でも、
query()で即座に結果が反映される。
5. 💻 コード全文(C++)
#include <bits/stdc++.h>
using namespace std;
const int N = 1 << 17; // 適当な2べき(大きめに)
int seg[2 * N];
int size;
int charToBit(char c) {
return 1 << (c - 'a');
}
void build(const string &s) {
size = 1;
while (size < s.size()) size <<= 1;
for (int i = 0; i < s.size(); ++i)
seg[i + size] = charToBit(s[i]);
for (int i = size - 1; i >= 1; --i)
seg[i] = seg[2*i] | seg[2*i+1];
}
int query(int l, int r) {
l += size;
r += size;
int res = 0;
while (l < r) {
if (l & 1) res |= seg[l++];
if (r & 1) res |= seg[--r];
l >>= 1; r >>= 1;
}
return __builtin_popcount(res);
}
void update(int i, char c) {
i += size;
seg[i] = charToBit(c);
while (i > 1) {
i >>= 1;
seg[i] = seg[2*i] | seg[2*i+1];
}
}
int main() {
string s = "abbaca";
build(s);
cout << query(1, 4) << endl; // 出力: 2
update(2, 'z');
cout << query(1, 4) << endl; // 出力: 3
}
💡 JavaScriptで模写すると(構造理解用)
function charToBit(c) {
return 1 << (c.charCodeAt(0) - "a".charCodeAt(0));
}
// セグメントツリーを配列で表現
let size = 1;
let seg = [];
function build(s) {
while (size < s.length) size <<= 1;
seg = new Array(size * 2).fill(0);
for (let i = 0; i < s.length; i++) {
seg[i + size] = charToBit(s[i]);
}
for (let i = size - 1; i >= 1; i--) {
seg[i] = seg[i * 2] | seg[i * 2 + 1];
}
}
function query(l, r) {
l += size;
r += size;
let res = 0;
while (l < r) {
if (l % 2) res |= seg[l++];
if (r % 2) res |= seg[--r];
l >>= 1;
r >>= 1;
}
return res.toString(2).split("1").length - 1; // popcount
}
function update(i, c) {
i += size;
seg[i] = charToBit(c);
while (i > 1) {
i >>= 1;
seg[i] = seg[i * 2] | seg[i * 2 + 1];
}
}
✅ まとめ
- セグメントツリーは「区間集約」に超便利
- 「ビット+OR+popcount」によって「種類数」を簡単に管理
- 文字列の差し替えも O(log N) でOK
💬 コメント